Log in
Download presentation
Presentation is loading. Please wait.

Similar presentations
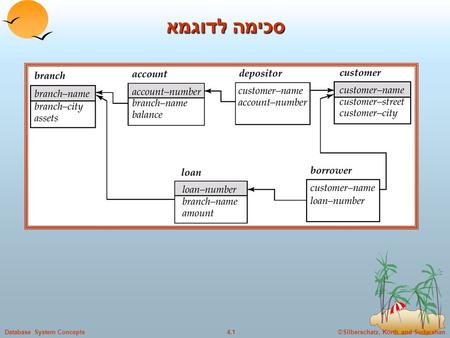
Presentation on theme: "כיצד גדל מין 1 בנוכחות מתחרהו, מין 2? איזוקלינת 0 של מין 1 שלאורכה dN 1 /dt = 0 מה משוואת הקו ? K 1 -N 1 -a 12 N 2 = 0 N 1 = K 1 -a 12 N 2 N2N2 Ν1Ν1 Κ1Κ1."— Presentation transcript:
1
כיצד גדל מין 1 בנוכחות מתחרהו, מין 2? איזוקלינת 0 של מין 1 שלאורכה dN 1 /dt = 0 מה משוואת הקו ? K 1 -N 1 -a 12 N 2 = 0 N 1 = K 1 -a 12 N 2 N2N2 Ν1Ν1 Κ1Κ1 תחרות בין - אוכלוסיתית / מינית היינו, כשמין 1 לבדו גידולו מתאפס כאשר N1=K1 כשהוא עם מתחרה הגידול יתאפס ב - N1 קטן יותר – כשמוחסר מ -K1 " שווי הערך " של N2, a 12 N 2
2
כיצד גדל מין 1 בנוכחות מתחרהו, מין 2? איזוקלינת 0 של מין 1 שלאורכה dN 1 /dt = 0 מה משוואת הקו ? K 1 -N 1 -a 12 N 2 = 0 N 1 = K 1 -a 12 N 2 N 2 =0 N 1 =K 1 N 1 =0 N 2 = K 1 /a 12 K 1 /a 12 N2N2 Ν1Ν1 Κ1Κ1 תחרות בין - אוכלוסיתית / מינית היכן תחתוך האיזוקלינה את הצירים ? איזוקלינת 0 של מין 1 הוא קו המחבר את כל הנקודות בהן N1 הוא בערך כזה שצפיפות מין 2 באותו זמן לא מאפשרת למין 1 לגדול לאורך איזוקלינת האפס נמצא מין 1 בשווי משקל
3
כללי הגידול בתנאי תחרות א. גידולו של כל מין נעצר באיזוקלינה שלו לפיכך הוא גדל רק בכוונה האיזוקלינה שלו ואם חרג ממנה, אוכלוסיתו חייבת לקטון ב. היות ומין 1 " סוחב " בכוון אפקי ומין 2 – אנכי הנתיב המשותף יהיה שקול שני הנתיבים העצמאיים N2N2 Ν1Ν1 Κ1Κ1 N 1 = K 1 -a 12 N 2 K 1 /a 12 Κ2Κ2 Ν1Ν1 N2N2 K 2 / a 21 N 2 = K 2 -a 21 N 1 Κ2Κ2 K 2 / a 21 K 1 /a 12 >K 2 K 2 /a 21 <K 1 איזוקלינת 0 של מין 1 איזוקלינת 0 של מין 2
4
N2N2 Ν1Ν1 Κ1Κ1 K 1 /a 12 Κ2Κ2 K 2 / a 21 מין 1 מנצח מין 2 נכחד K 1 /a 12 >K 2 K 1 >k 2.a 12 עכוב הגידול עקב ההפרעה התוך-מינית של מין 1 (K 1 ) גדול מהעיכוב שנגרם ע"י ההפרעה הבין-מינית של מין 2 על מין 1(K 2 a 12 ) K 2 /a 21 <K 1 K 1 a 21 >K 2 עכוב הגידול של מין 2 ע " י ההפרעה הבין - מינית של מין 1 על מין 2K 1 a 21 ) ) גדול מעכוב הגידול עקב ההפרעה התוך - מינית של מין 2 (K 2 ) איזו 1 איזו 2
5
N2N2 Ν1Ν1 Κ1Κ1 K 1 /a 12 Κ2Κ2 K 2 / a 21 מין 1 מנצח מין 2 נכחד K 1 /a 12 >K 2 K 1 >k 2.a 12 עכוב הגידול עקב ההפרעה התוך-מינית של מין 1 (K 1 ) גדול מהעיכוב שנגרם ע"י ההפרעה הבין-מינית של מין 2 על מין 1(K 2 a 12 ) K 2 /a 21 <K 1 K 1 a 21 >K 2 עכוב הגידול של מין 2 ע " י ההפרעה הבין - מינית של מין 1 על מין 2K 1 a 21 ) ) גדול מעכוב הגידול עקב ההפרעה התוך - מינית של מין 2 (K 2 ) K 1 /a 12 Κ1Κ1 Κ2Κ2 K 2 / a 21 N2N2 Ν1Ν1 מתי מין 1 יכחד ? K 1 /a 12 >K 2 K 1 >k 2.a 12 K 2 /a 21 >K 1 K 1 a 21 <K 2 קטן מין 1 נכחד מין 2 ל – K 2 איזו 1 איזו 2
6
K 1 /a 12 Κ1Κ1 Κ2Κ2 K 2 / a 21 Ν1Ν1 מין 1 נכחד מין 2 ל - 2 K המין בעל יכולת הפרעה בין - מינית חזקה ( כושר תחרות בין - מינית גבוה ) יגבר על המין בעל כושר תחרות בין - מינית נמוך N2N2 N2N2 K 1 /a 12 Κ2Κ2 Ν1Ν1 K 2 / a 21 Κ1Κ1 K 1 /a 12 >K 2 k 2.a 12 <K 1 K 2 /a 21 <K 1 K 1.a 21 >K 2 פרטי כל מין מתחרים חזק יותר עם פרטי המין השני מאשר בינם לבין עצמם. התחרות הבין - מינית חזקה מהתוך - מינית לתחרות הניצול מתווספת תחרות הפרעה - כל מין מרעיל הסביבה לשני יותר מלעצמו התוצאה תלויה ברכוזים ההתחלתיים שווי משקל רופף
7
כל מין מפריע לעצמו יותר משמפריע למתחרהו אף אחד לא יכול להכחיד את השני דו-קיום, קיום יחדיו, Coexistence N2N2 K 1 /a 12 Κ2Κ2 Ν1Ν1 K 2 / a 21 Κ1Κ1 התוצאה תלויה ברכוזים ההתחלתיים שווי משקל רופף Κ2Κ2 K 2 / a 21 N2N2 Ν1Ν1 Κ1Κ1 התוצאה תלויה ברכוזים ההתחלתיים שווי משקל רופף המין בעל יכולת הפרעה בין - מינית חזקה ( כושר תחרות בין - מינית גבוה ) יגבר על המין בעל כושר תחרות בין - מינית נמוך K 1 /a 12 Κ2Κ2 K 2 / a 21 Κ1Κ1 איזו 1 איזו 2 יציב לא K 2 / a 21 > Κ 1 K 2 > K 1. a 21 K 1 /a 12 > Κ 2 Κ 1 > Κ 2. a 12
8
סיכום הדמיות מודל לוטקה - וולטרה לתחרות בין - אוכלוסיתית היחסים הכמותיים בין ערכי הרוויה ומקדמי התחרות בתוך כל מין ובין המינים יקבעו את נתיבי הגידול של כל מין בנוכחות משנהו מין אחד יכחיד את משנהו, וישיג את ערך הרוויה שלו המין שריכוזו ההתחלתי גבוה ממשנהו, יכחיד את משנהו למעט כאשר הרכוזים ההתחלתיים זהים אז יושג דו - קיום, אך רופף שני המינים יגיעו לדו - קיום יציב, כ " א מתחת לערך הרוויה שלו r קובע את קצב השגת התוצאה, אך לא את התוצאה
9
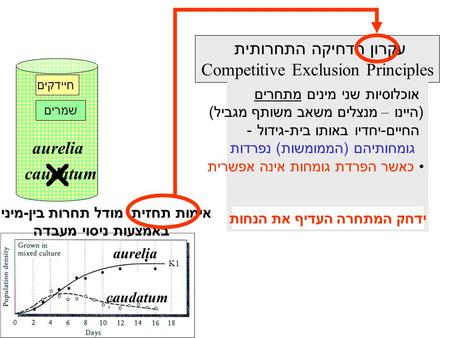
מודל מתמטי לתחרות בין - אוכלוסיתית שתי משוואות דיפרנציאליות סימולטניות N2N2 Ν1Ν1 Κ1Κ1 K 1 /a 12 Κ2Κ2 K 2 / a 21 איזו 1 תחזיות המודל היחסים בין ההפרעה העצמית להדדית קובעים את התוצאה, קצבי הגידול – את מהירות השגתה מין 1 יכחיד את מין 2 מין 2 יכחיד את מין 1 דו - קיום רופף בתלות ברכוזים התחלתיים דו - קיום יציב אימות תחזית באמצעות ניסוי מעבדה הדמייה גרפית של דינמיקת המודל המתמטי איזו 2
10
Paramecium סנדלית Gause, 1934 K1 K2 K1 מין 1 מין 2 P. aurelia P. caudatum 0 2 4 6 8 10 12 14 16 18 N גדלים בנפרד הכחדה תחרותית של caudatum ע " י aurelia
11
K2 K3 שווי משקל תחרותי יציב שני המינים מתחת לרוויה
12
שמרים חיידקים caudatum bursaria שווי משקל תחרותי יציב שני המינים מתחת לרוויה שני המינים גודלו במבחנה עם אספקת מזון קבועה – חיידקים ושמרים השמרים שקעו לתחתית ושם היו רוב bursaria והמין השני – caudatum, היה בעיקר בשאר המבחנה
13
שמרים חיידקים caudatum bursaria שמרים חיידקים caudatum bursaria בית גידול תת בית - גידול מונחים
14
שמרים חיידקים caudatum bursaria שמרים חיידקים caudatum bursariacaudatum בית גידול תת בית - גידול שמרים חיידקים bursaria מה קורה כשמגדלים כל מין במבחנה נפרדת ?
15
שמרים חיידקים caudatum bursaria שווי משקל תחרותי יציב שני המינים מתחת לרוויה שמרים חיידקים caudatum bursariacaudatum בית גידול תת בית - גידול שמרים חיידקים bursaria מבחנה חיידקים שמרים הגומחה האקולוגית הפרדת גומחות עקב תחרות הבסיסית הגומחה הממומשת חיידקים שמרים כל אחד משני המינים נזון משני מיני המזון הגומחה הממומשת
16
שמרים חיידקים caudatum bursaria שווי משקל תחרותי יציב שני המינים מתחת לרוויה שמרים חיידקים caudatum bursariacaudatum בית גידול תת בית - גידול שמרים חיידקים bursaria מבחנה חיידקים שמרים הגומחה האקולוגית הפרדת גומחות עקב תחרות הבסיסית הגומחה הממומשת ערבוב המבחנה חיידקים שמרים
17
חיידקים caudatum bursaria שווי משקל תחרותי יציב שני המינים מתחת לרוויה הפרדת גומחות עקב תחרות הגומחה הממומשת ערבוב המבחנה חיידקים שמרים caudatum bursaria בבית הגידול רוויה בגומחה הממומשת גם כשהמבחנה מעורבבת כל מין ניזון ממין מזון אחד היינו – נמצא בחלק הממומש של הגומחה הבסיסית שלו
18
גודל פריט המזון הגומחה האקולוגית Ecological Niche יעילות אמצעי ההגנה של המזון הגומחה הבסיסית Fundamental Niche של מין 1 הגומחה הבסיסית של מין 2 כאשר כל אחד מהמינים חי בבית גידול Habitat נפרד. הגומחה הממומשת של מין 2 כל מין יכחד מחלק ממרחב הגומחה הבסיסית ויוגבל בבלעדיות לגומחה הממומשת שלו – דו קיום יציב בבית הגידול או - אחד המינים יכחד מכל מרחב הגומחה הבסיסית – דחיקה תחרותית והם בעלי גומחה בסיסית חופפת ( מנצלים משאב משותף מגביל ) בית גידול - כתובת כאשר שני המינים באותו בית גידול - מקצוע הגומחה הממומשת Realized Niche של מין 1
19
גודל פריט המזון הגומחה האקולוגית כעל-נפח (hypervolume) רב-מימדי יעילות אמצעי ההגנה של המזון טמפרטו רה על-נפח רב-מימדי (כל מימד מייצג מקטע של תנאי סביבתי) בתוכו הפרטים מתרבים ושורדים והאוכלוסיה - שעור התחלופה 1 ולכן ברת-קיימא הגומחה הבסיסית
20
גודל פריט המזון הגומחה האקולוגית כעל-נפח (hypervolume) רב-מימדי יעילות אמצעי ההגנה של המזון טמפרטו רה על-נפח רב-מימדי (כל מימד מייצג מקטע של תנאי סביבתי) בתוכו הפרטים מתרבים ושורדים והאוכלוסיה - שעור התחלופה 1 ולכן ברת-קיימא גומחות ממומשות מין יכול למצוא בבית גידול מסוים רק חלק ממרחב גומחתו הבסיסית : מבחנה ללא שמרים הכילה רק חלק מהגומחה הבסיסית חלוקה על ציר אמצעי הגנה חלוקה על ציר גודל הפריט
Similar presentations
Similar presentations
© 2025 SlidePlayer.com. Inc.
All rights reserved.